Search
Close
Search
Advanced Search
Search Menu

Abstract

Frequency analysis of pulsating stars can be performed via several algorithms. Still, each of these methods has its own specific flaws which advocates for the use of as many tools as possible. However, the lack of simple programs with straightforward interface impedes such a goal. pdm13 is a new software dedicated to spectral analysis based on the phase dispersion minimization technique. Its graphical environment, combined with complementary tools, such as auto-segmentation, makes it a simple and powerful mean for frequency extraction. In this paper, a detailed description of the mathematical algorithms is presented. Then, we introduce the options and interface of pdm13. Finally, we compare the results from different case study using pdm13 and other programs.

methods: data analysis, techniques: photometric, stars: oscillations, stars: variables: RR Lyrae

1 INTRODUCTION

As a fundamental tool to study the internal structure of stars, asteroseismology has proven to be particularly relevant. Still, progress is limited by the data accuracy and by inherent discontinuities of ground-based observations. The improvements of investigation methods are essential to overcome such obstacles, even if these issues tend to vanish with space missions such as CoRoT and Kepler.

Frequencies and mode identification constitute an important part of the main data of asteroseismology. They can be obtained by performing a projection of a discrete photometric signal on a trigonometric basis. There are two different approaches to frequency extraction: the parametric and the non-parametric method. The first one is the most commonly used and referred to as a Fourier-based analysis as one fits a harmonic model function to the data. The second does not assume an a priori model for the photometric function. Period04 (Lenz & Breger 2005) is an example of the available instrument for such purpose based on parametric method. Stellingwerf's phase dispersion minimization (PDM) technique (Stellingwerf 1978) is an alternative to Fourier transform algorithms for frequency extraction. As underlined by its author (Stellingwerf 2011), this non-parametric method outmatches existing ones for specific cases, urging for complementary investigation via different algorithms. Unfortunately, the lack of graphical interface and simplicity prevents a widespread usage of PDM.

In this paper, we present a new graphical interfaced program based on the PDM method, pdm13. This application also includes new features such as auto-segmentation, Gauss–Newton least-squares fitting and cyclostationary modulation detection together with the usual set of tools provided by such programs like phase, residuals or significance plots. The current 1.0 version and sources are available at forge.oca.eu/trac/PDM13.

2 THEORY AND METHOD

2.1 PDM

PDM is a non-parametric approach for frequency extraction based on statistic methods and data folding. For each frequency, the phase diagram is computed and a mean curve is calculated. After dividing the diagram into bins, data spread around a mean curve is measured as
\begin{equation} \Theta _{{\rm PDM}}\equiv \frac{\left(\sum \limits _{j=1}^{B} (N_j-1){s_j}^2\right)\Bigg/\left(\sum \limits _{j=1}^B N_j-B\right)}{\left(\sum \limits _{i=1}^N (x_i - \overline{x})^2\right)/(N-1)}, \end{equation}
(1)
where
\begin{equation} s_j^2\equiv \frac{\sum \limits _{i = 1}^{N_j}(x_{ij}-\overline{x_j})^2 }{N_j - 1} \end{equation}
(2)
with B the number of bins, Nj the number of data sets in bin j, xij the observation x(ti) with bin index j, |$\overline{x_j}$| the average over a bin, N and |$\overline{x}$| the overall number of data and average.

For frequency that is not present in the data, we will find ΘPDM ≈ 1.

2.2 Auto-segmentation

As underlined by Stellingwerf (2011), the computation time is greatly reduced when performing a first frequency search using a small segment rather than over the whole data sets. Besides, aliases due to gaps can also be diminished by such an approach. Nevertheless, the previous version of PDM relied on a threshold value defined by the user to determine if the time span between two points was a significant gap. The auto-segmentation algorithm is able to detect automatically each segment allowing a more simple and precise process.

For a given set of N data points ni(ti;mi), where ti and mi are the respective time and magnitude, the idea is to compute the delay between two following data points Δti = ti + 1 − ti and to detect any discontinuities using the Lee & Heghinian test (Lee & Heghinian 1977).

This test is a Bayesian procedure applied to normally distributed series with a null hypothesis being the absence of discontinuities. We consider the following model:
\begin{equation} X_j = \left\lbrace \begin{array}{ll}\mu + \epsilon _j &\quad \mbox{}\mbox{} j = 1, 2, \ldots , \tau \\ \mu + \delta + \epsilon _j &\quad \mbox{}\mbox{} j = \tau +1, \ldots , n \end{array}\right., \end{equation}
(3)
where ϵj are random variables, independent and normally distributed, with null expectance value and a constant variance. The break point τ and the parameters μ and δ are unknown.
The method determines the a posteriori probability distribution function of the parameters τ and δ, considering their a priori distributions and supposing that the break time follows a uniform distribution. τ a posteriori distribution is computed as
\begin{equation} P(\tau | x)\propto \frac{\sqrt{\frac{n}{\tau (n-\tau )}}}{R(\tau )^{n-2}}, \end{equation}
(4)
\begin{equation} R(\tau ) = \frac{ \sum _{i = 1}^{\tau }(x_i-\overline{x_{\tau }})^2 + \sum _{i = \tau +1}^{n}(x_i-\overline{x_{n - \tau }})^2}{\sum _{i = 1}^{n}(x_i-\overline{x_{n}})^2}, \end{equation}
(5)
\begin{equation} \mbox{with } \overline{x_{\tau }} = \frac{1}{\tau }\sum _{i = 1}^{\tau }x_i \quad\mbox{ and }\quad \overline{x_{n-\tau }} = \frac{1}{n-\tau }\sum _{i = \tau +1}^{n}x_i. \end{equation}
(6)

Therefore, we can estimate the probability that a discontinuity occurs at time τ. However, the Lee & Heghinian algorithm's computation time increases rapidly for rich data sets. Thus, we have implemented a recursive method reducing the complexity to |$\mathcal {O}(n)$|⁠.

As this method broadens the spectral features from 1/T to 1/Tj, where T is the total time base and Tj the total time of the longest segment, we need to perform a second scan including gaps near the best candidate given by the first step.

2.3 Gauss–Newton algorithm

In former version of PDM, the amplitude associated to the best candidate frequency was the one of the mean curve. We have added a least-squares fitting algorithm which allows further investigation and comparison of the obtained value.

Considering the N-residuals function ri, of two variables A and ϕ (the amplitude and the phase of the fitting curve, respectively) (N ≥ 2), the aim is to find iteratively the minimum of the sum of squares as
\begin{equation} S(\boldsymbol {B}) = \sum _{i = 1}^{N}r_i(\boldsymbol {B})^2 \end{equation}
(7)
starting with an initial guess |$\boldsymbol {B^{(0)}} = (A^{(0)}, \phi ^{(0)})$| for A and ϕ, |$\boldsymbol {B^{(s+1)}}$| is given by
\begin{equation} \boldsymbol {B^{(s-1)}} - \boldsymbol {B^{(s)}} - ({bf J}_r^\top {bf J}_r)^{-1}\boldsymbol {B^{(s)}}, \end{equation}
(8)
\begin{equation} \mbox{where} \;{bf J}_r = \frac{\mathrm{\partial} {r_i}}{\mathrm{\partial} {B_j}}(\boldsymbol {B^{(s)}}) \;{\rm is\; the\; Jacobian\; matrix\; of\; } r. \end{equation}
(9)

After a first scan, the residuals are calculated using the Stobie method (Stobie 1970). One can choose to remove only the extracted frequency from the signal or the signal mean curve.

2.4 Modulation detection and Blazhko effect

pdm13 can search directly for modulation frequency, which is extremely interesting for detecting the Blazhko effect (Blazko 1907). A modulated signal is a cyclostationary process which means that its statistical properties present a periodicity as shown by equation (10):
\begin{equation} E[Y(t)] = m_y(t) = m_y(t+T), \end{equation}
(10)
where Y represents the magnitude and T the modulation period. While existing methods use specific functional forms to describe modulation (Szeidl & Jurcsik 2009; Benkő, Szabó & Paparó 2011), cyclostationarity does not impose an a priori model.

Based on this property, the program will divide the data in sub-segments and compute mean values for each of them. Then, the PDM algorithm will look for periodicity in the resulting file giving a best candidate for modulation frequency.

3 pdm13 INTERFACE

The graphical interface is divided in three parts.

  • Light curve module: within this module, the user can import, export, edit and plot the time string data.

  • PDM module: this module is dedicated to the extraction of frequencies – including multiple period and Blazhko modulation. As we have already mentioned, the PDM algorithm is used for this purpose. The user can also obtain a significance plot related to the extracted frequency – using the Beta function test or the Monte Carlo test.

  • Gauss–Newton module: in the third part, the Gauss–Newton algorithm performs a least-squares fit to obtain the amplitude and phase related to each selected frequency.

Besides, the Configuration menu allows more control on the automated parameters.

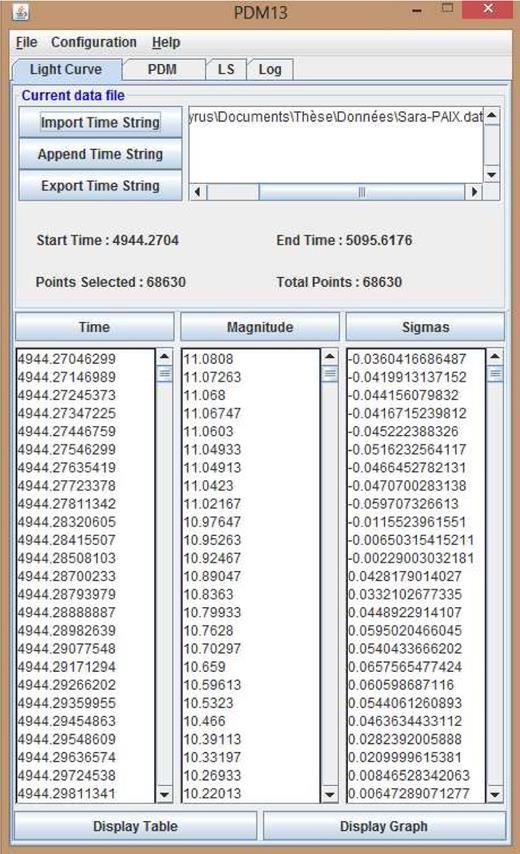
3.1 Light Curve tab

In this tab (Fig. 1), time series can be imported, exported, appended and edited. Furthermore, data points can be plotted using the Display Graph button.

Figure 1.
Light curve module.
Open in new tabDownload slide

Light curve module.

Each plot can be manipulated using directly the mouse to zoom on a specific area or by choosing the Select ViewPort or View all in the Zoom menu. Likewise, each graph can be printed or exported in PNG/EPS format using the Graph menu.

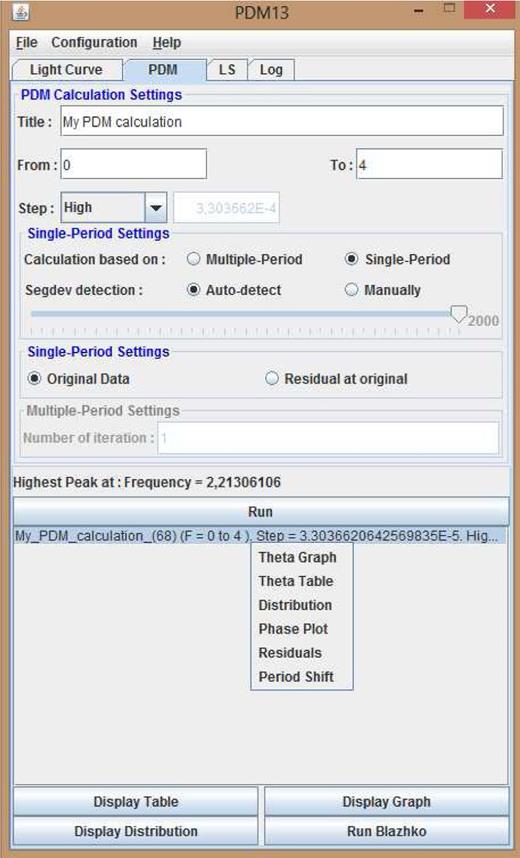
3.2 PDM tab

This tab is divided into two parts: a panel which contains the available settings and a list box where PDM results are displayed (see Fig. 2).

Figure 2.
PDM module.
Open in new tabDownload slide

PDM module.

In the first part called PDM Calculation Settings, the frequency range and step can be edited as well as the title of the theta plot. The step between each investigated frequency is automatically fixed according to the given data. A Custom option is available to set this option manually.

The panel on the one hand permits to program numerous loops in order to look for multiple periods. The number of loops has to be specified in the Multiple-Period Settings block. On the other hand, it enables the user to set his own parameters for the segment detection or to let the program work on its own as already discussed. In manual mode, the program will look for gaps greater than a specified multiple – defined by segdev – of the average time between each of the data points. Using this mode is particularly interesting when a single segment is needed to avoid important bias due to small time coverage.

After the first run, the corresponding residuals are calculated. By switching the Single-Period Settings to Residual at original, the algorithm looks for a significant period in the pre-whitened data from the selected tab in the list box. Moreover, the user can choose to add the extracted frequency with a given number of harmonics to the LS tab after each calculation.

For each analysis, a line is added to the list box. This line contains the name and the parameters used for the calculation. Different options are available when right clicking on one of the tabs. First, the Theta Graph and Theta Table can be displayed. Equivalent to the Fourier spectrum, their minimum shows an a priori significant frequency. The pop-up menu also gives access to the Distribution Plot and table as well as the Period-Shift graph – if these options have been activated in the Configuration menu.

The residuals obtained after the selected analysis can also be plotted using this menu. Finally, the phase plot of the light curve at the best candidate frequency can be represented using the Phase plot option as well as the fit curve by selecting Fit Curve in the Curves menu.

At the bottom of the panel, different buttons give direct access to some of the plot and table already mentioned. The Run Blazhko button starts a direct scan for modulation frequency. The resulting file will have a ‘[Blazhko]’ prefix in the list box.

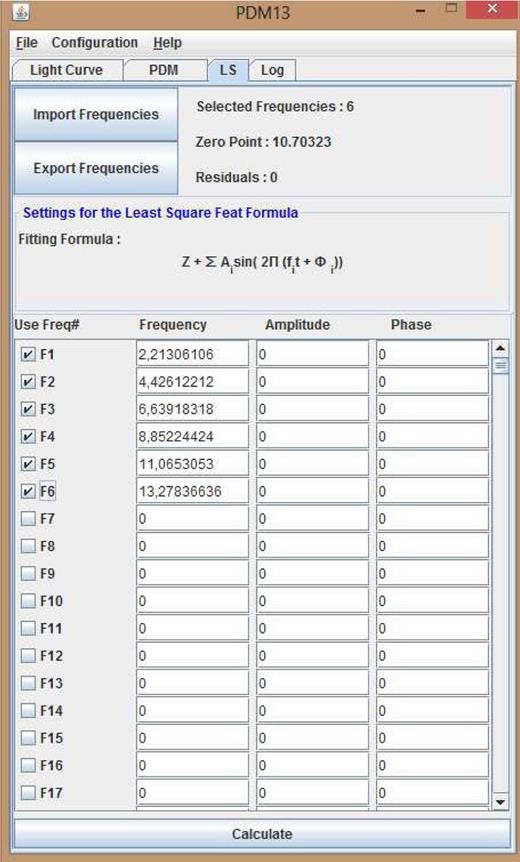
3.3 LS tab

Each frequency extracted, along with their harmonics, ends up in this part (Fig. 3). Frequencies, amplitudes and phases are imported or exported using the corresponding button. The Calculate button launches the least-squares fitting for all the selected items according to the formula specified in the upper panel. New frequencies can be added manually. Mathematical operations are accepted as long as they start with an = sign. For instance, in f2, the following line ‘ = 2*F1’ will be replaced by the double of the first frequency.

Figure 3.
Gauss–Newton module.
Open in new tabDownload slide

Gauss–Newton module.

Also, some information about the current fit are displayed such as Zero-Point, Selected Frequencies, Residuals.

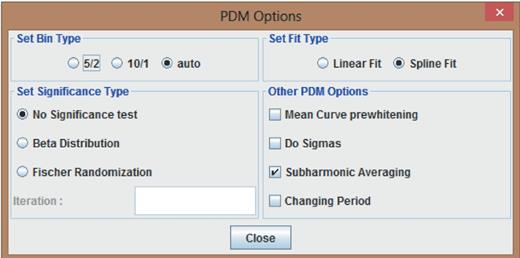
3.4 Menu bar

Along with the usual possibilities found in a menu bar – save, load, new project, import, export – the Configuration menu allows the user to have more control on the PDM process (Fig. 4).

Figure 4.
Option window.
Open in new tabDownload slide

Option window.

The Set Bin Type offers three possibilities: 10/1, 5/2, auto. The auto option will let the program choose by itself which type of bin should be used. If the 10/1 option is selected, 10 or a 100 bins will be used – depending on the number of data points – to cover a period with no overlap between each of the data points. The 5/2 option is similar except that there is a half coverage between each of the bins which is more convenient for data sets with less than 100 points and produces less noise.

The Set Fit Type can be set to Linear Fit or Spline Fit. The latter gives a smoother fit of the bin means.

Set Significance Type can be used in order to obtain a significance distribution for each theta value, the significance being a probability that a pure signal noise has produced a theta value as low or lower than the observed one. The Beta function test is based on Schwarzenberg-Czerny (Schwarzenberg-Czerny 1997) incomplete beta function given by equation (11) – where N is the total number of data points, M is the number of bins and Θ is the value of the PDM theta statistic – combined with a bandwidth correction (equation 12), as suggested by Press et al. (1992):
\begin{equation} \beta \left(\frac{N-M}{2}, \frac{M-1}{2} ; \frac{N-M}{N-1}\Theta \right), \end{equation}
(11)
\begin{equation} \beta _2 = 1 - (1 - \beta )^m, \end{equation}
(12)
where |$m = \frac{n_{\rm f}}{lpoints}$|⁠, with nf the number of frequency points and lpoints the number of points per spectral line. Still, the bandwidth correction is not fully determined by equation (12) as it depends on numerous details of the analysis. Thus, an alternative approach is the Monte Carlo test by Nemec & Nemec (Linnell Nemec & Nemec 1985) where the data order is randomized and the theta minimum obtained is an estimate of ‘pure noise’. Repeating this process many times gives a distribution of the noise-generated theta-mins.
In the Other PDM Options part, the data quality can be taken into account using the sigma values by selecting the Do Sigmas option. To avoid the sub-harmonic issue due to the detection of n-period periodic signal, the Subharmonic Averaging option performs a simplified significance test at each frequency and eventually replace the theta value by the average of the actual theta and the theta at half frequency. Finally, to detect slow period changes in the given data set, the Changing Period option can be activated. When a calculation is launched, the software opens dialog boxes where the period shift range and precision has to be defined according to equation (13), where β is a quantity given the dimension of d Myr−1 which is a unit of 1/365.25e6, P0 is the period obtained without the period shift change and the time t is zero at the middle of the current data sets:
\begin{equation} P = P_0 + \beta t. \end{equation}
(13)

4 CASE STUDY AND DISCUSSION

Stellingwerf presented two case studies of artificial data strings where the PDM algorithm outperforms the Lomb–Scargle technique (Stellingwerf 2011). We carry on this study by showing the effect of accurate segmentation on the outcome of the computation.

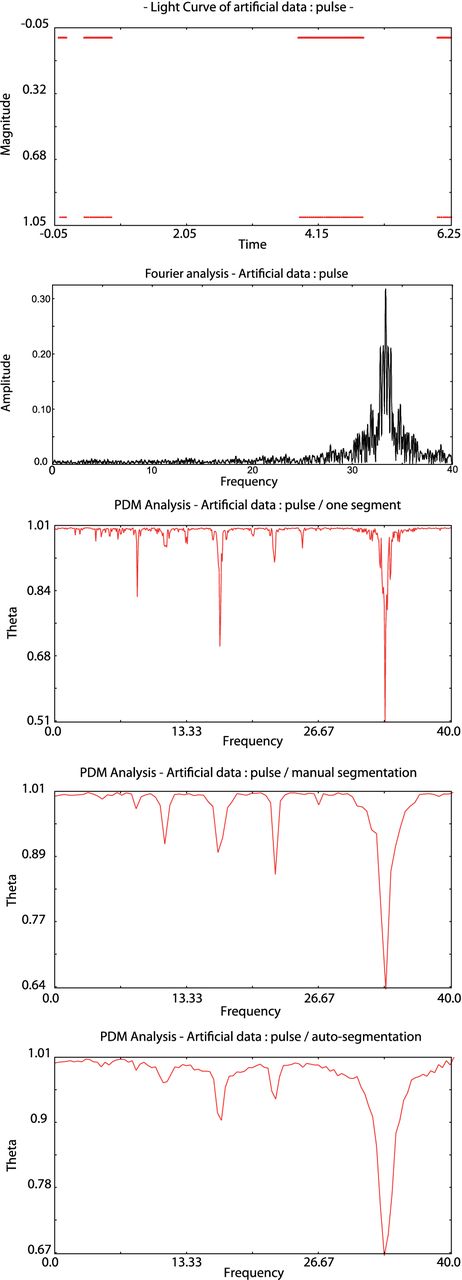
The first one is a series of narrow pulses with unevenly distributed gaps (Fig. 5). The following curves correspond, respectively, to the frequency analysis for a Fourier-type method, PDM with no segmentation, PDM with manual segmentation and pdm13 with auto-segmentation. The details of the auto-segmentation are shown in Table 1. It is clear, as already stated, that PDM curve is more precise with narrower spectral lines and less prominent side lobes. What is even more noticeable is that aliases are smaller when considering the auto-segmentation result.

Figure 5.
From top to bottom: Artificial data of several narrow pulses periodically spaced (T = 0.03 d) with unevenly distributed gaps; Fourier spectrum; pdm13 plot with no segmentation; pdm13 plot with manual segmentation; pdm13 plot with auto-segmentation.
Open in new tabDownload slide

From top to bottom: Artificial data of several narrow pulses periodically spaced (T = 0.03 d) with unevenly distributed gaps; Fourier spectrum; pdm13 plot with no segmentation; pdm13 plot with manual segmentation; pdm13 plot with auto-segmentation.

Table 1.

Auto-segmentation of artificial data: pulse.

Segment numberStart pointNumber of pointsTstartTrange
101260.0010.125
21264400.4070.439
356610333.8111.032
415992216.0190.22
Segment numberStart pointNumber of pointsTstartTrange
101260.0010.125
21264400.4070.439
356610333.8111.032
415992216.0190.22
Open in new tab
Table 1.

Auto-segmentation of artificial data: pulse.

Segment numberStart pointNumber of pointsTstartTrange
101260.0010.125
21264400.4070.439
356610333.8111.032
415992216.0190.22
Segment numberStart pointNumber of pointsTstartTrange
101260.0010.125
21264400.4070.439
356610333.8111.032
415992216.0190.22
Open in new tab

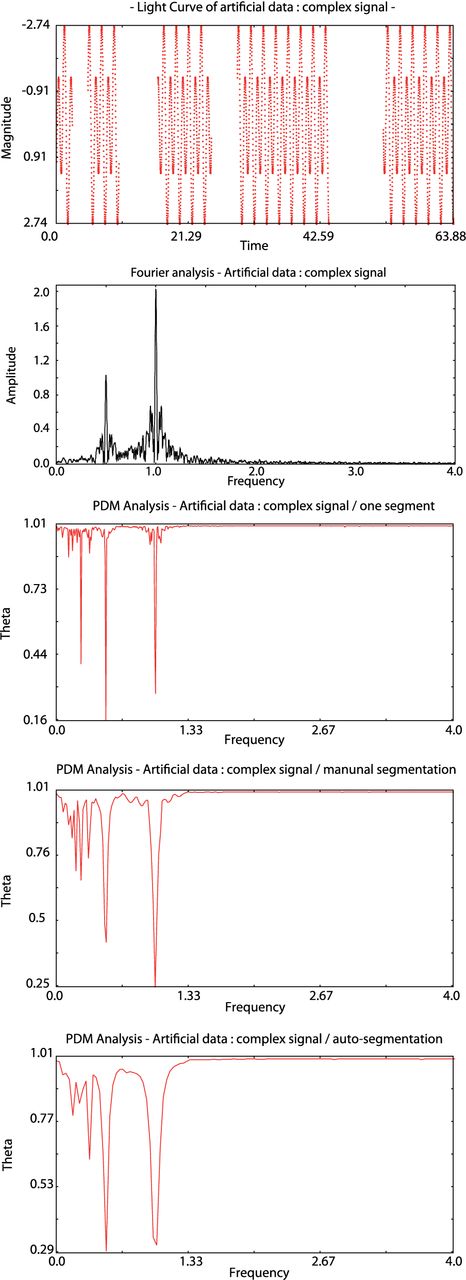
The second example was originally meant to show flaws in the Lomb–Scargle results in the case of a complex signal while PDM managed to obtain the accurate main frequency. We will push further this example by showing that adding gap in such case may lead to similar imprecise value unless the auto-segmentation option is used. The curve is shown in Fig. 6 along with the corresponding Fourier and pdm13 spectrum, without and with the auto-segmentation option. The results of the segment auto-detection are available in Table 2. As indicated, the manual segmentation and the Lomb–Scargle show an erroneous main period of 1 per day. Such an issue can be overcome by not performing segmentation but this will increase the calculation time.

Figure 6.
From top to bottom: Artificial data of complex signal made of two sinusoids (T1 = 1 d and $T_2 = \frac{1}{2}\; {\rm d}$) with unevenly distributed gaps; Fourier spectrum; pdm13 plot with no segmentation; pdm13 plot with manual segmentation; pdm13 plot with auto-segmentation.
Open in new tabDownload slide

From top to bottom: Artificial data of complex signal made of two sinusoids (T1 = 1 d and |$T_2 = \frac{1}{2}\; {\rm d}$|⁠) with unevenly distributed gaps; Fourier spectrum; pdm13 plot with no segmentation; pdm13 plot with manual segmentation; pdm13 plot with auto-segmentation.

Table 2.

Auto-segmentation of artificial data: complex signal.

Segment numberStart pointNumber of pointsTstartTrange
1025102.5
225150155
375286416.278.63
41616148029.0414.79
53096113552.5411.34
Segment numberStart pointNumber of pointsTstartTrange
1025102.5
225150155
375286416.278.63
41616148029.0414.79
53096113552.5411.34
Open in new tab
Table 2.

Auto-segmentation of artificial data: complex signal.

Segment numberStart pointNumber of pointsTstartTrange
1025102.5
225150155
375286416.278.63
41616148029.0414.79
53096113552.5411.34
Segment numberStart pointNumber of pointsTstartTrange
1025102.5
225150155
375286416.278.63
41616148029.0414.79
53096113552.5411.34
Open in new tab

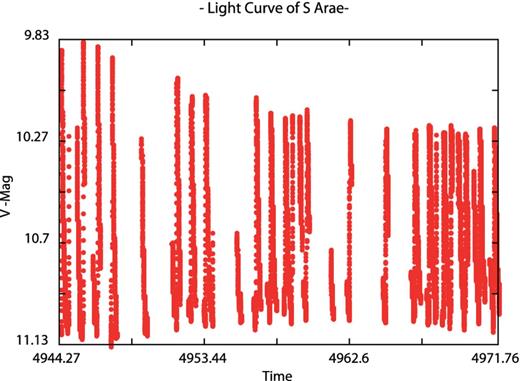
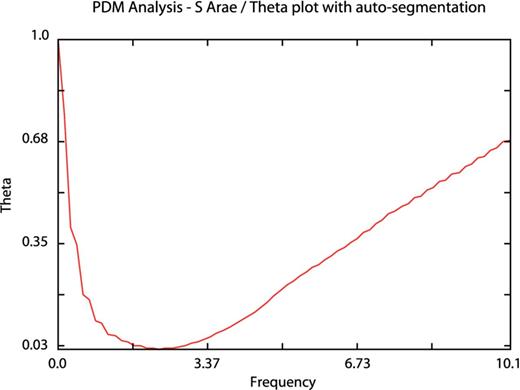
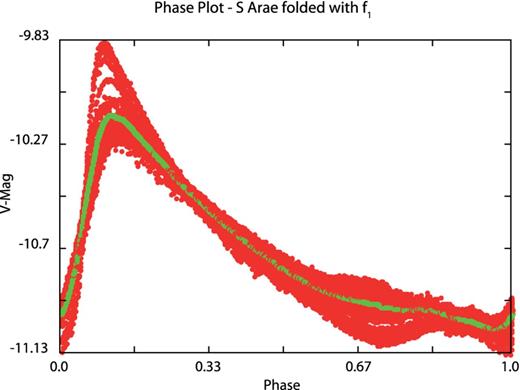
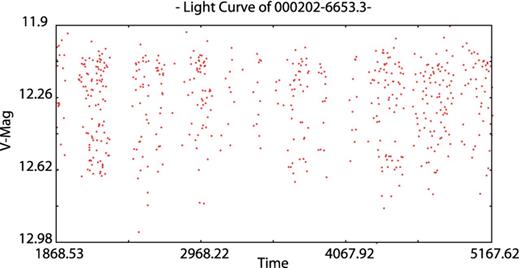
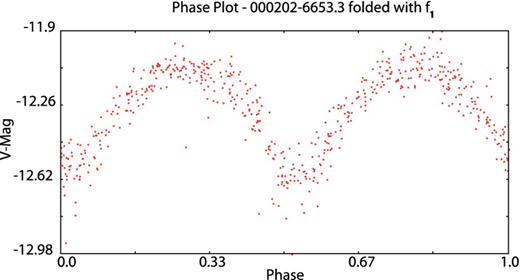
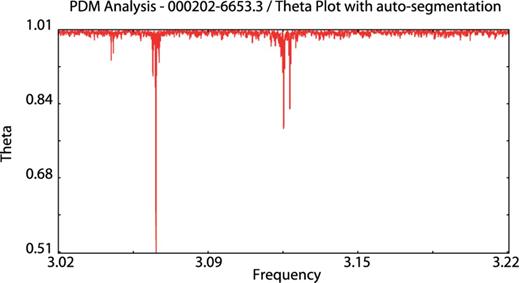
Our last test cases are the Blazhko RR Lyrae star S Arae (⁠|$\alpha = 17^{\rm h}59^{\rm m}10 {.\!\!^{\rm s}}73$|⁠, δ = −49°26′00|${^{\prime\prime}_{.}}$|45, J2000; Chadid et al. 2010) observed from Antarctica using the Photometer AntarctIca eXtinction (PAIX) telescope and the eclipsing binary star 000202−6653.3 (⁠|$\alpha = 0^{\rm h}02^{\rm m}02 {.\!\!^{\rm s}}0$|⁠, δ = −66°53′17|${^{\prime\prime}_{.}}$|9, J2000 with Vmax = 12.16 mag) from the ASAS Catalogue (Pojmanski 2002). These case studies focuses on pdm13 auto-segmentation ability (Tables 3 and 4). Even with a very high duty cycle for a ground-based observation site, S Arae light curve shows numerous gaps (Fig. 7). Running the algorithm using manual segmentation and a segdev value of about 500 leads to irrelevant results such as f1 = 1.1065 d− 1 ± 3.303 662E − 4 or f1 = 0.4426 d− 1 ± 3.303 662E − 4 showing the importance of this parameter in the PDM analysis. By performing an accurate and automated segmentation with the auto-segmentation option, we avoid such obstacle. Indeed, the algorithm was able to isolate 23 clusters ending up with f1 = 2.2129 d− 1 ± 3.303 662E − 4 (Fig. 8) as obtained by Chadid et al. with Period04. The Blazhko behaviour is clear in the phase plot folded with the main frequency (Fig. 9). The investigation for a modulation frequency leads to a value of fm = 0.1999 ± 3.303 662E − 4. Similarly, running pdm13 on 000202−6653.3 (Fig. 10) using one segment ends up with a main frequency f1 = 3.562 051 683 d− 1 ± 2.537 101E − 5 while the correct period of 3.062 081 498 d− 1 ± 2.537 101E − 5 is obtained using the auto-segmentation option (Figs 11 and 12).

Figure 7.
PAIX light curve of S Arae.
Open in new tabDownload slide

PAIX light curve of S Arae.

Figure 8.
Theta plot of S Arae using auto-segmentation.
Open in new tabDownload slide

Theta plot of S Arae using auto-segmentation.

Figure 9.
Folded PAIX light curve with main pulsation P1 (in red) and mean curve (in green).
Open in new tabDownload slide

Folded PAIX light curve with main pulsation P1 (in red) and mean curve (in green).

Figure 10.
Light curve of 000202−6653.3.
Open in new tabDownload slide

Light curve of 000202−6653.3.

Figure 11.
Folded 000202−6653.3 light curve with main pulsation P1.
Open in new tabDownload slide

Folded 000202−6653.3 light curve with main pulsation P1.

Figure 12.
Theta plot of 000202−6653.3 using auto-segmentation.
Open in new tabDownload slide

Theta plot of 000202−6653.3 using auto-segmentation.

Table 3.

Auto-segmentation of S Arae data.

SegmentNumber ofTstartTrange
numberStart pointpoints
105254944.270 4630.478 773
25255104945.264 850.486 643
310355014946.283 6920.466 146
415363754947.396 0190.363 356
519113574949.333 160.340 74
622685484951.238 5190.522 152
728164804952.233 160.451 782
832965734953.223 1250.553 935
938692674955.306 250.256 285
1041364924956.313 6230.466 666
1146287114957.198 090.589 966
1253396784958.208 2410.585 671
1360172944959.203 380.165 532
1463113914959.440 660.373 692
1567021744961.188 7850.158 981
1668764054962.178 0790.286 84
1772814684964.443 4950.346 366
1877496814966.213 6340.562 13
1984308604967.196 9790.612 361
2092909074968.155 1390.644 363
2110 1979004969.150 0350.638 946
2211 0979874970.134 780.702 176
2312 0848614971.1496 410.614 896
SegmentNumber ofTstartTrange
numberStart pointpoints
105254944.270 4630.478 773
25255104945.264 850.486 643
310355014946.283 6920.466 146
415363754947.396 0190.363 356
519113574949.333 160.340 74
622685484951.238 5190.522 152
728164804952.233 160.451 782
832965734953.223 1250.553 935
938692674955.306 250.256 285
1041364924956.313 6230.466 666
1146287114957.198 090.589 966
1253396784958.208 2410.585 671
1360172944959.203 380.165 532
1463113914959.440 660.373 692
1567021744961.188 7850.158 981
1668764054962.178 0790.286 84
1772814684964.443 4950.346 366
1877496814966.213 6340.562 13
1984308604967.196 9790.612 361
2092909074968.155 1390.644 363
2110 1979004969.150 0350.638 946
2211 0979874970.134 780.702 176
2312 0848614971.1496 410.614 896
Open in new tab
Table 3.

Auto-segmentation of S Arae data.

SegmentNumber ofTstartTrange
numberStart pointpoints
105254944.270 4630.478 773
25255104945.264 850.486 643
310355014946.283 6920.466 146
415363754947.396 0190.363 356
519113574949.333 160.340 74
622685484951.238 5190.522 152
728164804952.233 160.451 782
832965734953.223 1250.553 935
938692674955.306 250.256 285
1041364924956.313 6230.466 666
1146287114957.198 090.589 966
1253396784958.208 2410.585 671
1360172944959.203 380.165 532
1463113914959.440 660.373 692
1567021744961.188 7850.158 981
1668764054962.178 0790.286 84
1772814684964.443 4950.346 366
1877496814966.213 6340.562 13
1984308604967.196 9790.612 361
2092909074968.155 1390.644 363
2110 1979004969.150 0350.638 946
2211 0979874970.134 780.702 176
2312 0848614971.1496 410.614 896
SegmentNumber ofTstartTrange
numberStart pointpoints
105254944.270 4630.478 773
25255104945.264 850.486 643
310355014946.283 6920.466 146
415363754947.396 0190.363 356
519113574949.333 160.340 74
622685484951.238 5190.522 152
728164804952.233 160.451 782
832965734953.223 1250.553 935
938692674955.306 250.256 285
1041364924956.313 6230.466 666
1146287114957.198 090.589 966
1253396784958.208 2410.585 671
1360172944959.203 380.165 532
1463113914959.440 660.373 692
1567021744961.188 7850.158 981
1668764054962.178 0790.286 84
1772814684964.443 4950.346 366
1877496814966.213 6340.562 13
1984308604967.196 9790.612 361
2092909074968.155 1390.644 363
2110 1979004969.150 0350.638 946
2211 0979874970.134 780.702 176
2312 0848614971.1496 410.614 896
Open in new tab
Table 4.

Auto-segmentation of 000202−6653.3.

SegmentStart pointNumber ofTstartTrange
numberpoints
10191868.525 7880.990 11
2191052033.890 15237.643 88
3124382439.899 22124.752 79
4162242620.545 1160.973 82
518622744.919 7114.003 48
6188582818.923 83225.600 01
724623107.919 248.002 65
824893146.915 7565.000 62
925713276.728 050
1025823356.578 373.0075
11260103382.574 4432.940 71
1227043526.901 3628.008 03
1327413584.860 650
14275203615.824 2261.895 43
15295243700.590875.930 75
16319153849.922 9763.015 05
17334124084.586 5655.936 76
18346804228.930 63269.614 14
19426934564.919 18307.606 38
20519514933.9213233.700 66
SegmentStart pointNumber ofTstartTrange
numberpoints
10191868.525 7880.990 11
2191052033.890 15237.643 88
3124382439.899 22124.752 79
4162242620.545 1160.973 82
518622744.919 7114.003 48
6188582818.923 83225.600 01
724623107.919 248.002 65
824893146.915 7565.000 62
925713276.728 050
1025823356.578 373.0075
11260103382.574 4432.940 71
1227043526.901 3628.008 03
1327413584.860 650
14275203615.824 2261.895 43
15295243700.590875.930 75
16319153849.922 9763.015 05
17334124084.586 5655.936 76
18346804228.930 63269.614 14
19426934564.919 18307.606 38
20519514933.9213233.700 66
Open in new tab
Table 4.

Auto-segmentation of 000202−6653.3.

SegmentStart pointNumber ofTstartTrange
numberpoints
10191868.525 7880.990 11
2191052033.890 15237.643 88
3124382439.899 22124.752 79
4162242620.545 1160.973 82
518622744.919 7114.003 48
6188582818.923 83225.600 01
724623107.919 248.002 65
824893146.915 7565.000 62
925713276.728 050
1025823356.578 373.0075
11260103382.574 4432.940 71
1227043526.901 3628.008 03
1327413584.860 650
14275203615.824 2261.895 43
15295243700.590875.930 75
16319153849.922 9763.015 05
17334124084.586 5655.936 76
18346804228.930 63269.614 14
19426934564.919 18307.606 38
20519514933.9213233.700 66
SegmentStart pointNumber ofTstartTrange
numberpoints
10191868.525 7880.990 11
2191052033.890 15237.643 88
3124382439.899 22124.752 79
4162242620.545 1160.973 82
518622744.919 7114.003 48
6188582818.923 83225.600 01
724623107.919 248.002 65
824893146.915 7565.000 62
925713276.728 050
1025823356.578 373.0075
11260103382.574 4432.940 71
1227043526.901 3628.008 03
1327413584.860 650
14275203615.824 2261.895 43
15295243700.590875.930 75
16319153849.922 9763.015 05
17334124084.586 5655.936 76
18346804228.930 63269.614 14
19426934564.919 18307.606 38
20519514933.9213233.700 66
Open in new tab

5 CONCLUSION

The different examples presented in this paper show that a spectral analysis based solely on the Fourier-type method can lead to incorrect conclusions. Such assessment advocates for complimentary frequency extraction tools. To achieve such a goal, these tools need to be simple and powerful to allow a widespread use. pdm13 reaches this aim by combining a graphical interface with automated processes. We have showed how these can outperform existing software on specific cases.

One of the main feature, the auto-segmentation based on the Lee & Heghinian's technique, is originally intended to detect one major change in the data sets. Still our recursive approach, which was first meant to reduce computation time, permits to detect multiple discontinuities. Consequently, we were able to obtain an accurate segmentation greatly reducing aliases and enhancing the result curve.

REFERENCES

Benkő
J. M.
, 
Szabó
R.
, 
Paparó
M.
. , 
MNRAS
, 
2011
, vol. 
417
 pg. 
974
 
Crossref
Search ADS
 
Blazko
S.
. , 
Astron. Nachr.
, 
1907
, vol. 
175
 pg. 
327
 
Crossref
Search ADS
 
Chadid
M.
, 
Vernin
J.
, 
Mekarnia
D.
, 
Chapellier
E.
, 
Trinquet
H.
, 
Bono
G.
. , 
A&A
, 
2010
, vol. 
516
 pg. 
L15
 
Crossref
Search ADS
 
Lee
A. F. S.
, 
Heghinian
M.
. , 
Technometrics
, 
1977
, vol. 
19
 pg. 
503
 
 
Lenz
P.
, 
Breger
M.
. , 
Commun. Asteroseismol.
, 
2005
, vol. 
146
 pg. 
53
 
Crossref
Search ADS
 
Linnell Nemec
A. F.
, 
Nemec
J. M.
. , 
AJ
, 
1985
, vol. 
90
 pg. 
2317
 
Crossref
Search ADS
 
Press
W. H.
, 
Teukolsky
S. A.
, 
Vetterling
W. T.
, 
Flannery
B. P.
. , 
Numerical Recipes in C. The Art of Scientific Computing
, 
1992
Cambridge
Cambridge Univ. Press

Google Scholar

OpenURL Placeholder Text

 
Pojmanski
G.
. , 
Acta Astronomica
, 
2002
, vol. 
52
 pg. 
397
 
 
Schwarzenberg-Czerny
A.
. , 
ApJ
, 
1997
, vol. 
489
 pg. 
941
 
Crossref
Search ADS
 
Stellingwerf
R. F.
. , 
ApJ
, 
1978
, vol. 
224
 pg. 
953
 
Crossref
Search ADS
 
Stellingwerf
R. F.
. 
McWilliam
A.
. , 
RR Lyrae Stars, Metal-Poor Stars, and the Galaxy
, 
2011
Pasadena, CA
The Observatories of the Carnegie Institution of Washington
pg. 
47
 

Google Scholar

OpenURL Placeholder Text

 
Stobie
R. S.
. , 
Observatory
, 
1970
, vol. 
90
 pg. 
20
 
 
Szeidl
B.
, 
Jurcsik
J.
. , 
Commun. Asteroseismol.
, 
2009
, vol. 
160
 pg. 
17
 
Crossref
Search ADS
 
© 2014 The Authors Published by Oxford University Press on behalf of the Royal Astronomical Society
Issue Section:
Article
Download all slides